도심이란 여러개의 하중을 하나의 집중하중으로 치환할때 써먹는 정의입니다.
평면에서 도심은 무게 중심이라고 말할수 있습니다.
도심값은 단면1차 모멘트 값에서 단면의 전체 면적으로 나누어 구할수 있습니다.

단면 1차 모멘트의 정의는

따라서 단면의 도심을 구하고 싶다면, 단면 1차모멘트 값을 계산한 후 전체 단면적으로 나누어주면 됩니다.
이를 수식으로 표현하면 다음과 같습니다.
단면 1차모멘트 값 Qx =∫ydA= A1y1 + A2y2 + A3y3 + A4y4 ..... = Ay
이때, A1 = 미소단면1의 단면적
y1 = x축으로부터 미소단면1의 도심까지의 y거리
A2 =미소단면2의 단면적
y2 = x축으로부터 미소단면2의 도심까지의 y거리
A3 = 미소단면3의 단면적
y3 = x축으로부터 미소단면3의 도심까지의 y거리
A4 =미소단면4의 단면적
y4 = x축으로부터 미소단면4의 도심까지의 y거리
A = 단면적 전체의 넓이(A1+A2+A3+A4+...)
y= x축으로 부터 전체 단면의 도심까지의 y거리
따라서 단면 1차 모멘트를 통해 구한 단면의 도심값은 다음과 같습니다.

예제1) 다음 2차 함수로 된 곡선의 도심을 찾으시오.


step1. 미소면적 dA 정의하기
dA는 미소 직사각형의 면적이므로 다음과 같이 나타낼 수 있습니다.

Step2. 전체면적 A구하기
A = ∫ dA
= ∫ ydx = ∫ h·(1−x^2/b^2)dx -> 0에서 b까지 적분하면
= 2bh/3
Step3. 단면 1차모멘트 Qx , Qy 값 구하기
위의 식을 이용하여 단면 1차모멘트의 정의를 이용하면 다음과 같습니다.

이때, 주의할점은 이때 y에 들어가는 값은 x축으로부터 미소면적 dA(직사각형)의 도심까지의 거리이기 때문에 y가 아닌 절반인 y/2 값이 들어 간다는 점 입니다. 이 점을 참고하여 Qx, Qy에 대한 계산을 마무리하면 다음과 같습니다.


step4. 단면 1차모멘트 값에서 전체면적을 나눠 도심 구하기
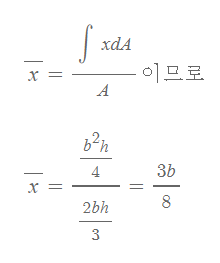

'일반기계기사 > 1. 재료역학' 카테고리의 다른 글
| 원형 축 설계하기 과정1 _ SFD & BMD (0) | 2023.01.17 |
|---|---|
| 모어의 원(Mohr's circle) (0) | 2023.01.09 |
| 2023년 1과목: 재료 역학 필기정리 (1/2) (0) | 2023.01.04 |
| [2022년 1회] 필기 기출문제 해설강의 | 재료역학 | 일반기계기사 홍교수 (0) | 2022.12.16 |
| 재료역학 정의 (2) | 2022.12.12 |